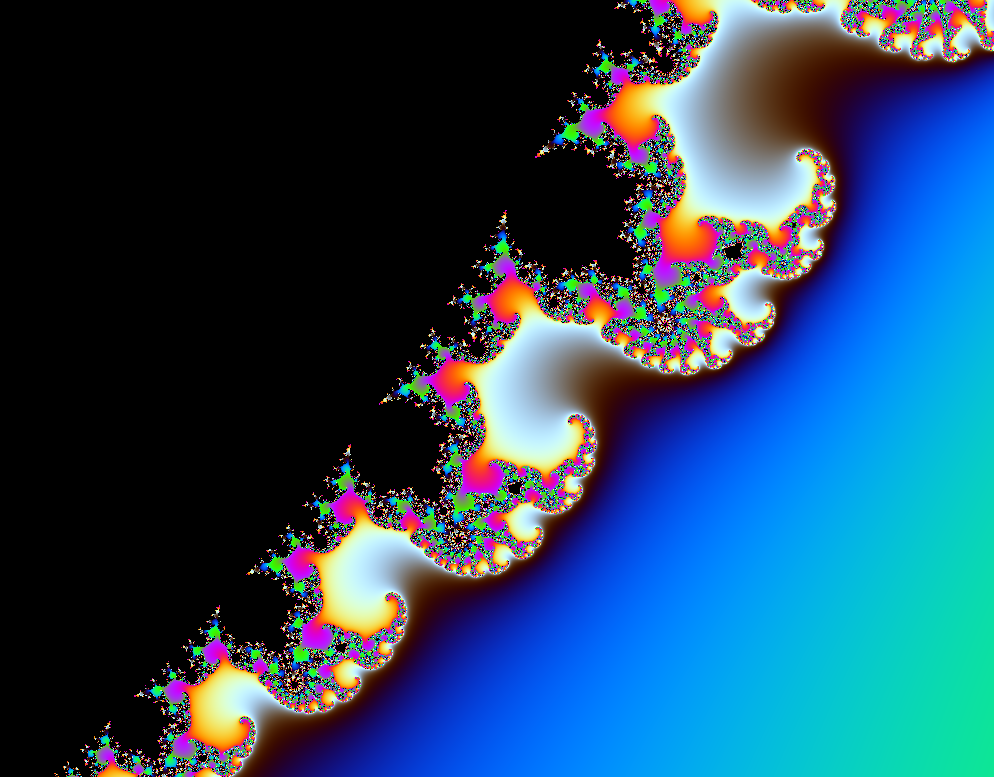
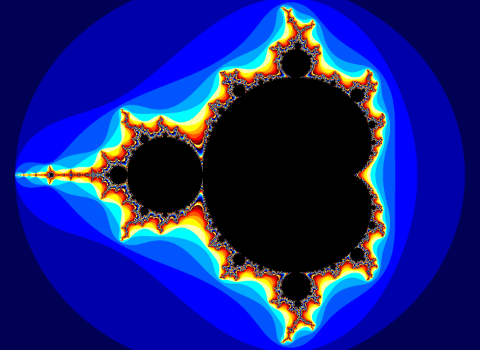
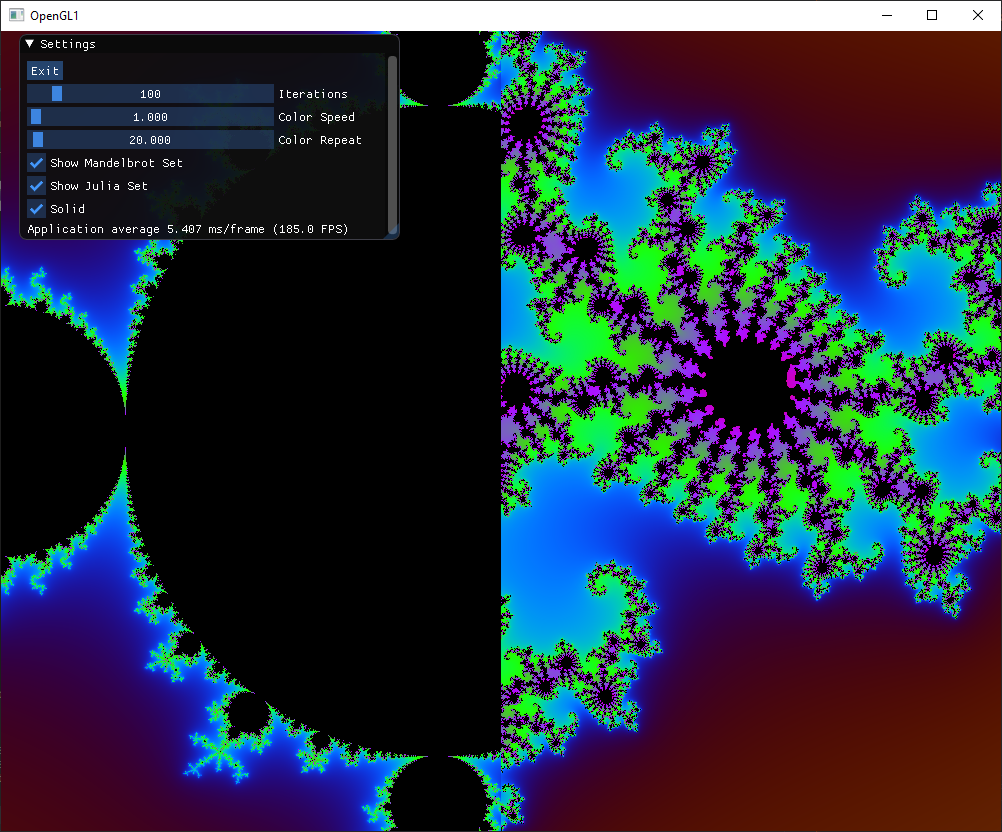
I will be guiding you through the process of making your own fractal explorer in this post, showcasing the structures of the Mandelbrot and Julia sets, as well as the relationship between them. We will be building off of the knowledge and progress of previous posts, so I urge you to first read my posts about the Mandelbrot set, Mandelbrot set Explorer, and Julia sets if you haven’t already. At the end it will display something like this:
VAOs and VBOs
To program, we’ll start where we left off with our Mandelbrot explorer program. The final code for this can be copied from here and we will be updating our Shader class code to this. The first step is to create some VAOs and VBOs for the “Julia Screen.” The code for this can be seen here:
glm::vec2 julia_ratio = glm::vec2(0.5, 1.0);
float julia_vertices[] =
{
1.0f - 2 * julia_ratio.x, julia_ratio.y, 0.0f,
1.0f, -julia_ratio.y, 0.0f,
1.0f, julia_ratio.y, 0.0f,
1.0f, -julia_ratio.y, 0.0f,
1.0f - 2 * julia_ratio.x, julia_ratio.y, 0.0f,
1.0f - 2 * julia_ratio.x, -julia_ratio.y, 0.0f,
};
Shader shader_julia(vertex_fractal, fragment_julia);
unsigned int julia_vao, julia_vbo;
glGenVertexArrays(1, &julia_vao);
glGenBuffers(1, &julia_vbo);
glBindVertexArray(julia_vao);
glBindBuffer(GL_ARRAY_BUFFER, julia_vbo);
glBufferData(GL_ARRAY_BUFFER, sizeof(julia_vertices), julia_vertices, GL_STATIC_DRAW);
glEnableVertexAttribArray(0);
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0);Remember to delete julia_vao and julia_vbo afterwards:
glDeleteVertexArrays(1, &julia_vao); glDeleteBuffers(1, &julia_vbo);
Julia_ratio is the screen ratio as compared to the whole window and shader_julia is the shader we will be using to render the Julia set. The fragment shader code (fragment_julia) can be copied from here:
Shaders
const char* fragment_julia = "#version 450 core\n"
"in vec3 FragPos;\n"
"uniform vec4 transform;\n"
"uniform int max_iter;\n"
"uniform float color_offset;\n"
"uniform float color_repeat;\n"
"uniform vec2 c;\n"
"uniform bool solid;\n"
"out vec4 FragColor;\n"
"void main()\n"
"{\n"
" vec2 z = vec2(FragPos) * transform.zw + transform.xy;\n"
" float r = 20.0;\n"
" float iter;\n"
" for(iter = 0; iter < max_iter; iter++)\n"
" {\n"
" z = vec2(z.x*z.x - z.y*z.y, 2*z.x*z.y) + c;\n"
" if(length(z) > r) break;\n"
" }\n"
" if(iter == max_iter)\n"
" if(solid)\n"
" FragColor = vec4(0, 0, 0, 1);\n"
" else\n"
" discard;\n"
" float dist = length(z);\n"
" float frac_iter = log(log(dist) / log(r)) / log(2);\n"
" float m = sqrt((iter - frac_iter) / max_iter);\n"
" FragColor = sin(vec4(0.2, 0.4, 0.6, 1) * m * color_repeat + color_offset) * 0.5 + 0.5;\n"
"}\0";This code is nearly identical to that of the Mandelbrot set. The only difference is that z is initially set to the position and c is a uniform input that we will be giving to the shader that determines the Julia set (there is also a bool solid which says whether the solutions to the set are transparent or black).
Julia Position
To keep track of this c value and other settings we will be using these global variables (yes I know they are bad practice but all of the code is pretty much in one file, so it is not a big deal):
glm::vec2 julia_pos; glm::vec2 mouse_pos; glm::vec4 transform;
Notice how we have made the transform a global, this is necessary. We will also keep track of these variables instantiated in main:
bool julia_solid = true, show_julia = true, show_fractal = true;
To keep track of the mouse position we will be using this GLFW callback:
static void cursor_position_callback(GLFWwindow* window, double xpos, double ypos)
{
mouse_pos.x = (float)xpos;
mouse_pos.y = (float)ypos;
}Don’t forget to set this callback for GLFW:
glfwSetCursorPosCallback(window, cursor_position_callback);
This mouse position will update the c value (julia_pos) here in the GetInputs method:
if (glfwGetKey(window, GLFW_KEY_SPACE) == GLFW_PRESS)
{
julia_pos.x = mouse_pos.x / Screen_Width * 2 - 1;
julia_pos.y = -mouse_pos.y / Screen_Height * 2 + 1;
julia_pos.x *= transform.z;
julia_pos.y *= transform.w;
julia_pos.x += transform.x;
julia_pos.y += transform.y;
}This first puts the mouse position onto a scale from -1 to 1 in each direction and transforms it to “fractal space,” so to speak. In other words, it finds the corresponding position of the mouse in the Mandelbrot set. When the space bar is pressed this will happen, but you can make it occur when the mouse is pressed instead with this code:
if (glfwGetMouseButton(window, GLFW_MOUSE_BUTTON_LEFT) == GLFW_PRESS)
ImGUI Code
These variables will also be editable with ImGUI using this code:
ImGui::Checkbox("Show Mandelbrot Set", &show_fractal);
ImGui::Checkbox("Show Julia Set", &show_julia);
ImGui::Checkbox("Solid", &julia_solid);Updating Shaders and Rendering
Finally, the code for rendering both fractals can be seen here:
if (show_fractal)
{
shader_fractal.Use();
shader_fractal.SetVec4("transform", transform);
shader_fractal.Setf("color_offset", time * color_speed);
shader_fractal.Setf("color_repeat", color_repeat);
shader_fractal.SetInt("max_iter", max_iter);
glBindVertexArray(fractal_vao);
glDrawArrays(GL_TRIANGLES, 0, 6);
}
if (show_julia)
{
shader_julia.Use();
shader_julia.SetVec4("transform", transform);
shader_julia.Setf("color_offset", time* color_speed);
shader_julia.Setf("color_repeat", color_repeat);
shader_julia.SetInt("max_iter", max_iter);
shader_julia.SetVec2("c", julia_pos);
shader_julia.SetInt("solid", julia_solid);
if (show_fractal)
{
glBindVertexArray(julia_vao);
}
else
{
glBindVertexArray(fractal_vao);
}
glDrawArrays(GL_TRIANGLES, 0, 6);
}Final Result
The final code can be found here and here is a video of the final result: